Une structure mécanique porteuse est un ensemble de solides agencés de manière organisée destiné à supporter des actions mécaniques importantes. Les poutres sont des éléments constitutifs de structures porteuses, et la sollicitation en flexion est une sollicitation mécanique très souvent rencontrées.



L’étude de cas proposée porte sur de simples poutres en flexion 3 points, de même longueur, mais de différents matériaux et de différentes sections.
Poutre au repos sur 2 appuis ponctuels distants de 500 mm (différentes sections de poutres à expérimenter) :
Modèle Poutre, au repos, sur 2 appuis ponctuels :
Modèle Poutre en flexion 3 points :
d = flèche maximale (déplacement maximal)
Les sections des poutres étant toutes contenues dans un carré de 10 x 10 mm, le but est de comparer le comportement sous charge des différentes poutres en termes de flèche et de contraintes mécaniques et de faire ressortir l’influence des sections d’une part (à matériau identique) et l’influence des matériaux (à section identique).
![]() = 80 min
= 80 min
Etape 1 - Créer la poutre avec SolidWorks
![]() Créer une nouvelle pièce.
Créer une nouvelle pièce.
Sur le plan de face, créer une nouvelle esquisse et esquisser la section de la poutre centrée sur l’origine (utiliser la fonction Rectangle par son centre)
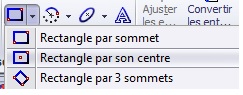
Coter l'esquisse jusqu'à obtenir une esquisse noire totalement contrainte.
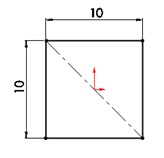
![]() Une fois l’esquisse totalement contrainte, réaliser une fonction extrusion Plan milieu de 500mm, de sorte à ce que le futur volume soit symétrique par rapport au plan d’esquisse.
Une fois l’esquisse totalement contrainte, réaliser une fonction extrusion Plan milieu de 500mm, de sorte à ce que le futur volume soit symétrique par rapport au plan d’esquisse.
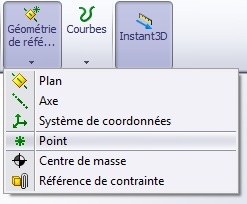
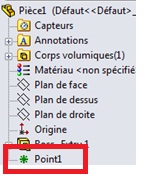
![]() Une fois le volume poutre extrudé, créer un point au centre de la surface supérieure de la poutre. Ce point sera utilisé par la suite pour simuler l’application d’une force sur la poutre.
Une fois le volume poutre extrudé, créer un point au centre de la surface supérieure de la poutre. Ce point sera utilisé par la suite pour simuler l’application d’une force sur la poutre.
![]() Enregistrer ce fichier pièce dans un dossier Simulation flexion poutre sous le nom Poutre section carrée 10x10x500.
Par la suite, pour les autres poutres à créer, les nom des fichiers seront similaires mais dépendront de la géométrie de la poutre.
Enregistrer ce fichier pièce dans un dossier Simulation flexion poutre sous le nom Poutre section carrée 10x10x500.
Par la suite, pour les autres poutres à créer, les nom des fichiers seront similaires mais dépendront de la géométrie de la poutre.
![]() Créer trois autres fichiers avec les profils suivants toujours pour une longueur de 500 mm :
Créer trois autres fichiers avec les profils suivants toujours pour une longueur de 500 mm :
Etape 2 - Relever les caractéristiques de la poutre
![]() Dans l'arborescence de gauche, faire un clic droit sur Matériau, puis Editer le Matériau. Dans la première bibliothèque, les matériaux à tester sont soit l'acier non allié C35 ou l'alliage d'aluminium EN-AW 5052
suivant le tableau du DR et Appliquer.
Dans l'arborescence de gauche, faire un clic droit sur Matériau, puis Editer le Matériau. Dans la première bibliothèque, les matériaux à tester sont soit l'acier non allié C35 ou l'alliage d'aluminium EN-AW 5052
suivant le tableau du DR et Appliquer.
![]() Dans le menu supérieur, sélectionner Outils / Evaluer et Propriétés de masse.
Dans le menu supérieur, sélectionner Outils / Evaluer et Propriétés de masse.
![]() Compléter le tableau Caractéristiques des poutres du DR en renseignant les caractéristiques de la poutre.
Compléter le tableau Caractéristiques des poutres du DR en renseignant les caractéristiques de la poutre.
![]() Attention :
Attention :
Etape 3 - Simuler la flexion de la poutre
![]() Cliquer sur l'onglet Simulation et créer une nouvelle étude de type statique.
Cliquer sur l'onglet Simulation et créer une nouvelle étude de type statique.
![]() Faire un clic droit sur le nom de la pièce et sélectionner Traiter comme une poutre.
Faire un clic droit sur le nom de la pièce et sélectionner Traiter comme une poutre.
Faire ensuite un clic droit sur Groupe de connexions, puis Modifier et Calculer (toutes). 2 connexions doivent en résulter. Ce processus permet de définir les limites du modèle poutre simulé (extrémités de poutre).
Explication de la simulation:
Nous simulons la flexion de la poutre avec un effort au centre. La première extrémité de la poutre (à gauche) ne pourra que pivoter pendant la déformation (pas de translation possible). La deuxième extrémité de la poutre (à droite) pourra pivoter pendant la déformation et pourra se translater mais uniquement longitudinalement (suivant la longueur de la poutre) car la poutre se rétracte du fait de la flexion.
![]() Faire un clic droit sur Déplacements imposés puis Géométrie fixe pour définir la manière dont peuvent se déplacer les extrémités de la poutre (les 2 connexions).
Faire un clic droit sur Déplacements imposés puis Géométrie fixe pour définir la manière dont peuvent se déplacer les extrémités de la poutre (les 2 connexions).
Au niveau de la connexion 1, l’extrémité de la poutre ne pourra pas se translater et ne pourra que pivoter pendant la déformation. Pour cela définir Immobile (pas de translation) et sélectionner la connexion puis valider.
Faire de nouveau un clic droit sur Déplacements imposés puis Géométrie fixe pour définir la manière dont peut se déplacer la deuxième extrémité de la poutre.
Au niveau de la connexion 2, l’autre extrémité de la poutre ne pourra que pivoter et se translater longitudinalement (simple appui ponctuel) : il faut donc bloquer 2 translations. Pour cela sélectionner Utiliser une géométrie de référence, sélectionner la 2eme connexion. Sélectionner le plan de droite (arbre de création), appuyer sur les icônes bloquant les translations dans la direction 2 du plan et suivant la normale au plan.
![]() Faire un clic droit sur Chargements externes pour définir la force sollicitant la poutre.
Faire un clic droit sur Chargements externes pour définir la force sollicitant la poutre.
Choisir le point 1 comme point d’application (géométrie de référence créé précédemment) puis le plan de droite (qui va contenir la force).
Sélectionner ensuite la direction 2 du plan pour définir la direction de la force et inverser au besoin pour définir le bon sens de celle-ci. Définir dans un premier temps l’intensité de la force à 5 N (correspondant au poids d’une masse de 0.5 Kg suspendue au centre de la poutre).

![]() Définir ou modifier le matériau de la poutre (acier non allié C35 ou l'alliage d'aluminium EN-AW 5052).
Pour cela faire un clic droit sur le nom de la pièce (icône poutre dans l’arbre de simulation).
Définir ou modifier le matériau de la poutre (acier non allié C35 ou l'alliage d'aluminium EN-AW 5052).
Pour cela faire un clic droit sur le nom de la pièce (icône poutre dans l’arbre de simulation).
Pensez à Appliquer avant de quitter.
![]() Exécuter la simulation.
Exécuter la simulation.
![]() Consulter les résultats et compléter le tableau du DR en relevant la contrainte maximale en Mpa et la flèche maximale en mm.
Consulter les résultats et compléter le tableau du DR en relevant la contrainte maximale en Mpa et la flèche maximale en mm.
![]() Répéter la simulation pour une charge de 10N, 15N et 20N et pour les différentes poutres.
Répéter la simulation pour une charge de 10N, 15N et 20N et pour les différentes poutres.
![]() = 15 min
= 15 min
![]() Comparer et commenter les courbes de la déformation :
Comparer et commenter les courbes de la déformation :
![]() Indiquer vos deux noms en haut à gauche du document réposnes.
Indiquer vos deux noms en haut à gauche du document réposnes.
![]() Enregistrer ou générer votre compte rendu en format pdf.
Enregistrer ou générer votre compte rendu en format pdf.
Renommer le fichier avec vos deux prénoms.
Copier votre fichier pdf dans le repértoire Restiution de devoirs du répertoire classe sur le réseau.
![]() = 15 min
= 15 min
La déformation en flexion d'une poutre se détermine à l'aide de la relation suivante :
|
|
Avec :
|
Le moment quadratique d’une section de poutre (par rapport à un axe) caractérise l’influence de la géométrie de cette section sur les contraintes et les déformations d’une poutre en flexion ou torsion.
![]() Question 1 - Sur une feuille, calculer les moments quadratiques des poutres n° 1, 3 et 4.
Question 1 - Sur une feuille, calculer les moments quadratiques des poutres n° 1, 3 et 4.
Question 2 - Calculer les déformations de ces 3 poutres avec une intensité de l'effort que vous choisirez. Le module de Young (ou module d’élasticité longitudinale) du matériau sera relevé sur SolidWorks. Comparer vos résultats avec ceux issus des simulations.