Implantation du motoréducteur

1 - Détermination de l’effort

= 50 min

On souhaite déterminer l’effort à appliquer sur le curseur (support de vitre) en C pour permettre la levée de la vitre.

Cet effort n’est pas nécessairement constant pendant toute la phase de levée, car les forces de frottement dans les coulisses sont proportionnelles à la longueur de vitre « en prise » dans les coulisses.

Une simulation a permis de déterminer que l’effort maxi se crée dans la position haute, juste avant la fermeture de la vitre. On étudie donc l’équilibre de l’ensemble S = {vitre + curseur} en position haute, avant fermeture.

Hypothèses :

• Solides indéformables.
• Problème plan (0,x,y).
• Masse de l’ensemble S : m_S =3,5 kg.
• Force linéaire de frottement dans les coulisses verticales : 0,04 N/mm.
• Force linéaire de frottement au niveau du joint lécheur horizontal : 0,037 N/mm.
• Accélération de la pesanteur : g = 9,81 m/s².
• α = 15°.
• R(O,x,y,z) : repère lié au bâti.
• R₁(G,x₁,y₁ ,z₁) : repère lié à la vitre.

Bilan des actions mécaniques extérieures exercées sur S :



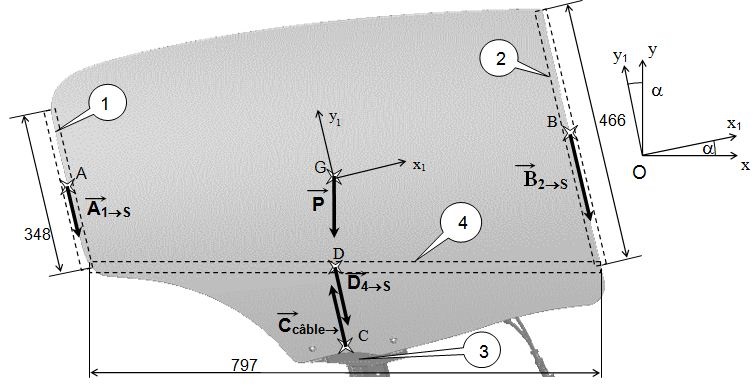
Attention : sur le schéma les actions de liaison en C dues à l’action du rail sur le curseur ne sont pas représentées (cf. dans le bilan {T_3→S}_C).

• En A, centre de la zone de contact entre la vitre et la coulisse gauche 1, les actions mécaniques de contact sont modélisées par le glisseur _A{T_1→S} dont la résultante est parallèle à y₁ :

• En B, centre de la zone de contact entre la vitre et la coulisse droite 2, les actions mécaniques de contact sont modélisées par le glisseur _B{T_2→S} dont la résultante est parallèle à y₁.
• En C, centre de la liaison glissière d’axe y₁ entre le curseur et le rail de guidage 3, lesactions mécaniques de contact sont modélisées par le torseur _C{T_3→S}. Cette liaison est supposée parfaite.
• Egalement en C, point d’ancrage du câble qui actionne le curseur, les actions mécaniques de contact sont modélisées par le glisseur _C {T_câble→S}.

• En D, centre de la zone de contact « horizontale » entre la vitre et le joint lécheur 4, les actions mécaniques de contact sont modélisées par le glisseur _D{T_4→S} .

• En G, centre de gravité de l’ensemble, l’action de la pesanteur est modélisée par le glisseur {T_pes→S}_G

Remarque : un torseur glisseur est un torseur dont le moment est nul et la résultante (force) n'est pas nulle.

 

Pour l'ensemble des torseurs vous présenterez leurs expressions vectorielles et analytiques.

Question 1 - Quelle est la longueur de vitre « en prise » avec la coulisse droite ?

   Observer comment a été calculé la force A_1→S  et écrit du torseur  {T_A1→S} _A vous allez vous en inspiré pour la question suivante.

Question 2 - Sachant que la force de frottement pour les coulisses verticales est de 0,04 N/mm, donner les coordonnées de la force B_2→S correspondant à ces frottements. Ecrire le torseur en B : {T_B2→S}_B dans le repère R₁.

Question 3 - Calculer la norme du poids de l’ensemble S.

Question 4 - Donner l’expression de {T_pes→S}_G dans R.

Question 5 - Donner l’expression de {T_pes→S}_G dans R₁.

Question 6 - Donner les degrés de liberté de la liaison glissière d’axe (C,y₁), dans le repère R₁.

Question 7 - En déduire dans le repère R₁ l’expression du torseur des actions mécaniques transmissibles par la glissière d’axe (C,y₁) : {T_3→S}_C.

Question 8 - Compte tenu du fait que le problème est dans le plan (O,x₁,y₁), quelles sont les composantes de {T_3→S}_C qui sont nulles ?

On étudie l’équilibre de S sous l’effet de toutes les actions mécaniques extérieures qui lui sont appliquées.

Question 9 - Donner l’expression du PFS sous forme de torseurs (ne pas développer, ne pas déplacer les torseurs en un point).

Question 10 - En exploitant uniquement le théorème de la résultante en projection sur y₁, déterminer la force sur le curseur nécessaire à la levée : F_C.

 

2 - Détermination du couple C_T

= 20 min

Choisir un motoréducteur permettant d’actionner la vitre en répondant au cahier des charges.

Quels que soient les résultats trouvés dans la partie 1, on estime la valeur de la force de levée en fin de course (avant fermeture) à : Fc = 100 N.

Schéma de principe du lève vitre

       

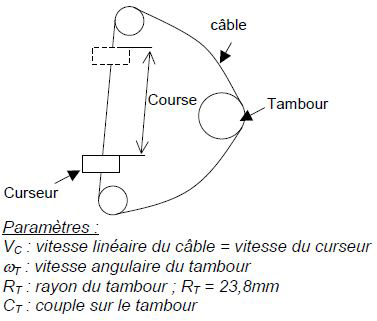
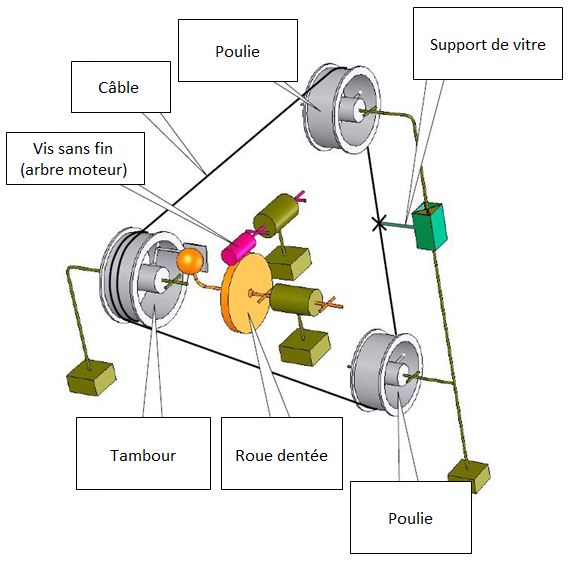
Question 11 - Quelle est la nature du mouvement du tambour par rapport à la portière et du curseur (support de vitre) par rapport à la portière ?

Question 12 - En vous appuyant sur le schéma de principe ci-dessus, en déduire l’expression littérale de la vitesse linéaire Vc du câble en fonction des paramètres fournis (Tous les paramètres n’interviennent pas nécessairement).



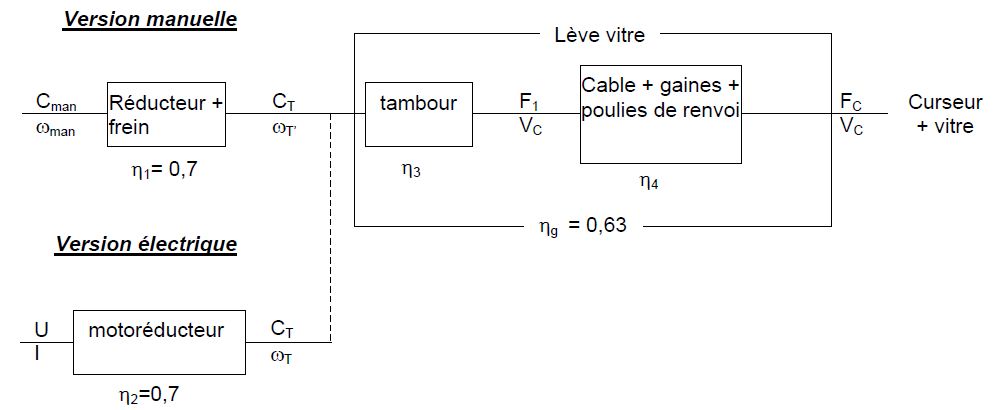
Question 13 - En exploitant les données sur la chaîne de transmission de puissance, donner l’expression littérale de la puissance Ps en sortie du lève-vitre fonction de la puissance Pe en entrée et du rendement.

Rappel :  Pour un mouvement de rotation, la puissance P = C.ω. De même pour un mouvement de translation, la puissance P = F.V.

Question 14 - En vous servant du rappel précédent, remplacer les éléments de l’expression littérale de la Question 13 pour faire apparaître les efforts et les vitesses.

Question 15 - Déduire des questions précédentes l’expression littérale du couple C_T à appliquer sur le tambour. Faire l’application numérique.

 

3 - Détermination de la vitesse N_T

= 20 min

Hypothèse : le mouvement de rotation fourni par le motoréducteur est uniforme (ω_T = constante). Par conséquent la vitesse de translation du curseur aussi (V_C = constante).

Question 16 - Sachant que la course du curseur est de 437 mm, calculer la vitesse Vc du câble pour obtenir une levée de vitre en 3,5 s. Vous donnerez votre résultat en m/s.

Question 17 - A l'aide de l'expression littérale de la Question 12, calculer en rad/s la vitesse angulaire du tambour ω_T pour obtenir une levée de vitre en 3,5 s. En déduire N_T en tr/min.

 

4 - Choix du motoréducteur satisfaisant

= 20 min

Courbes caractéristiques des motoréducteurs Brose type D

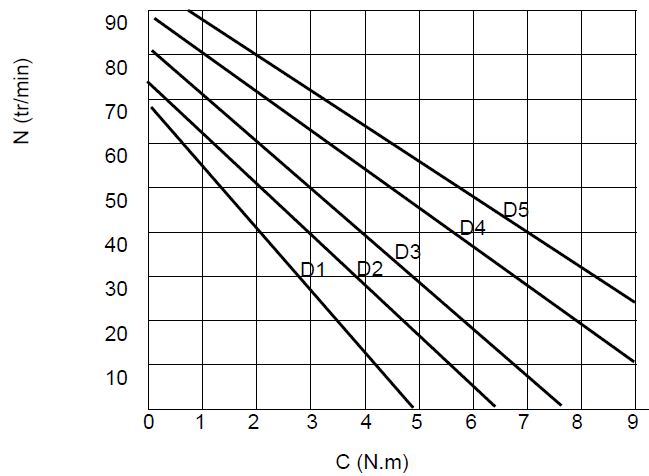
Question 18 - En exploitant les résultats précédents, placer mentalement sur la courbe le point de fonctionnement correspondant à C_T et N_T. Quels sont les motoréducteurs qui conviennent pour la phase de levée ?

Question 19 - Selon les conditions climatiques et l'état du guidage en translation de la vitre, l'effort nécessaire peut légèrement augmenter. Quel choix de motoréducteur feriez-vous pour éviter un blocage du système ?